Essay: Matrices for 3D applications - Translation & Rotation
Translation & Rotation
A discussion of 4x4 matrices in the context of a 3D application.
1. Transformations
Transformations are an important part of every 3D application. This knol discusses the different types of transformations and what you can do with them.The most important transformations you will encounter are :
- World transformation
: change the scale, translation and rotation of an object. The
transformation can be the result of a concatenation (multiplication) of
several transformation matrices. A world transformation is usually a
unique transformation for each 3D object in the scene.
- View transformation : This transformation is used to transform the entire scene. The transformation transforms all the vertices and expresses them in a new local axis that is defined by the camera, with the camera position as origin, the direction the camera is looking at as z-vector and the up vector of the camera as y-vector. (x-vector can be derived from the cross product of z & y vector). Usually the same view transformation is applied to all the objects in the scene.
- Projection transformation : Can add a perspective projection to the scene or an orthogonal projection. This transformation uses homogenous coordinates.
- Aligning an object with the camera (object is always in the same relative position from the camera)
- A hierarchy of transformations can be used to transform objects with parent child relationships (for example the rotation of a steering wheel in a moving car)
2. Introduction to 4x4 matrices
The 4x4 matrix is a very powerful tool. In this first part of the article we discuss why we need 4x4 matrices and homogeneous coordinates and how to apply a transformation to a vector.A homogeneous coordinate is a 3D coordinate with an extra fourth coordinate w added to it. For example if we have a 3D coordinate [2,3,4] , the homogeneous coordinate is formed by [2,3,4,1].
When we want to convert a homogeneous coordinate back to a normal 3D coordinate we simply apply the following formula :
This
means that a 3D coordinate can be represented with an infinite number
of homogeneous coordinates. The homogeneous coordinate [4,6,8,2] is also
a representation of the 3D coordinate [2,3,4].
The first row, first column of the result is obtained by calculating the dot product of the coordinate (first row) with the first column of the matrix :
2.1 Translation
The first example is the translation of a point. To translate a point we need to multiply the homogeneous representation of the vector with the 4x4 matrix. The translation vector [tx,ty,tz] will be placed on the last row of the transformation matrix :
Every
point that is multiplied with the given matrix will be translated with
the amount [tx,ty,tz]. To multiply a homogeneous coordinate with a
matrix we need to multiply the vector with each column of the
matrix. We can look at the point as a 1x4 matrix (1 row, 4 columns). The
multiplication of a 1x4 matrix with a 4x4 matrix gives a 1x4 matrix as
result (a homogeneous coordinate).
The first row, first column of the result is obtained by calculating the dot product of the coordinate (first row) with the first column of the matrix :
The first row, second column of the result is obtained by calculating the dot product of the coordinate (first row) with the second column of the matrix :
The first row, third column of the result is obtained by calculating the dot product of the coordinate (first row) with the third column of the matrix :
The first row, fourth column of the result is obtained by calculating the dot product of the coordinate (first row) with the fourth column of the matrix :
The final result of the transformation is :
This result is as expected but it is important to note that this transformation would not work without homogeneous coordinates. It could come across as overkill to use matrices for this simple transformation. However the next section will demonstrate the usage of matrices to rotate a vertex round the origin.
This result is as expected but it is important to note that this transformation would not work without homogeneous coordinates. It could come across as overkill to use matrices for this simple transformation. However the next section will demonstrate the usage of matrices to rotate a vertex round the origin.
3. Rotation matrices for Euler angles (rotation about X,Y and Z axis)
Euler angles can be used to describe the rotation of an object in 3D space. It is customary in a 3D application to split the rotation up in 3 parts : yaw (rotation about Y axis) , pitch (rotation about z axis) and roll (rotation about X asis).Other disciplines use other conventions, such as ZXZ, which is know as Cardan angles. There are 12 possible arrangements for euler angles, and it is important to know which one is used to describe the rotation of an object.
3.1. Rotation about the Z axis
We start with this rotation matrix because it corresponds to a rotation in 2D. The rotation matrix will only change the x and y component of the vertex :The formula for this rotation is :
If we want to present this in matrix form we expand the formula :
OpenGL defines the matrix in column major order and for OpenGL the matrix would be :
DirectX stores the matrix in row major order so we need to switch rows and columns :
T = My * Mz * Mx
or :
It is off course possible to calculate this resulting transformation T symbolically. The multiplication uses the same technique as shown in the beginning of the article.
OpenGL defines the matrix in column major order and for OpenGL the matrix would be :
DirectX stores the matrix in row major order so we need to switch rows and columns :
3.2. Rotation about the X axis
We use a right handed axis system :
The transformation matrix we create will rotate vertices with the right hand rule. Point your thumb in the positive direction of the rotation axis and the fingers indicate the positive rotation angle :
The rotation about the X axis is similar to the rotation about the Z axis :| The matrix as defined for DirectX is : |
3.3. Rotation about the Y axis
Finally , the rotation about the Y axis is given by :| The matrix as defined for DirectX is : |
3.4. Rotation order
If the order of rotation is changed, the resulting transformation will be different. If we want to use a yaw pitch roll transformation (Y Z X ) we need to multiply the 3 transformation matrices in that order.T = My * Mz * Mx
or :
It is off course possible to calculate this resulting transformation T symbolically. The multiplication uses the same technique as shown in the beginning of the article.
Essay: Matrices for 3D applications - Translation & Rotation
![]() Reviewed by EssayPapers
on
14:07
Rating:
Reviewed by EssayPapers
on
14:07
Rating:












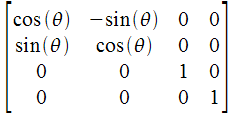













No comments: